

On the first recursion, call move n-1 disks from source rod to auxiliary using destination rod. While making recursion calls we just have to assume that we will get the result.Ī similar way this problem can be solved: Recursion problems consist of the base cases, recursion calls where we don’t have to worry about the result and small a calculation. This problem can be solved using recursion. Solution:ĭisclaimer: Don’t jump directly to the solution, try it out yourself first. No disk can be placed on top of smaller disk.Įxplanation: Moving disks from one rod to another using an auxiliary rod takes these steps.Įxplanation: Moving disks from one rod to another using an auxiliary rod takes these steps.The objective of this problem is to move the stack of disks from the initial rod to another rod, following these rules: Initially, all the disks are placed on one rod, one over the other in ascending order of size similar to a cone-shaped tower.”

This is how you solve the Tower of Hanoi using recursion.Problem Statement: “The Tower of Hanoi, is a mathematical problem which consists of three rods and multiple disks. The formula to calculate the number of steps for n disks is : (2^n)-1 The output for n=5 is : Take disk 1 from rod A to rod C

#Programming hanoi towers code
You can run the code for any number of disks. We can understand the process using the following illustration. The output for the code is: Take disk 1 from rod A to rod C The base case in our code is when we only have one disk. Let’s begin with understanding the two main parts of the code to solve the Tower of Hanoi problem. Implementing the Solution to Tower of Hanoi in Java In the function we write, we will print the movement of the disks. However, we can use this to create a function that does it recursively. Of course, you can’t do it like this because of the constraints. Take the disk number 1 and 2 to tower B.To get the three disks over to the final tower you need to : We solve this question using simple recursion. Let’s name the towers as A,B,C and the disks as 1,2,3. Theoretical Solution to the Tower of Hanoi Problem Since you can only move one disk at a time, the disk you move will have to be at the top of its tower. To do this you have an extra tower, it is known as helper/auxiliary tower. You can only move one disk at a time and never place a smaller disk over a larger disk. So you need to move all the disks from the first tower over to the last. A larger disk can not be placed on a smaller disk. While moving the disks, certain rules must be followed. Problem Statement Move all the disks stacked on the first tower over to the last tower using a helper tower in the middle. It is associated with a legend of a Hindu temple where the puzzle was supposedly used to increase the mental discipline of young priests. Tower of Hanoi Default Setupįun fact : This game was invented by a French mathematician Édouard Lucas in the 19th century. The disks are stacked in such a way that a disk is always over a disk bigger than itself. Initially all the disks are stacked on the first tower. The disks can be moved from one peg to another.
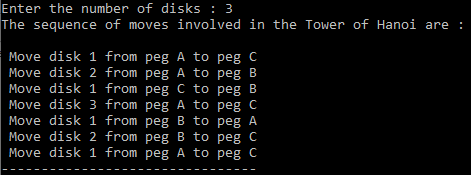
The problem setup consists of three rods/pegs and n disks. The Tower of Hanoi is a classic problem in the world of programming.


 0 kommentar(er)
0 kommentar(er)
